깊이 우선 탐색 Depth first search (DFS)
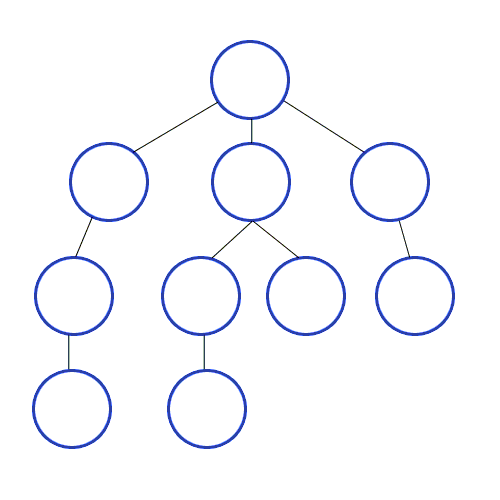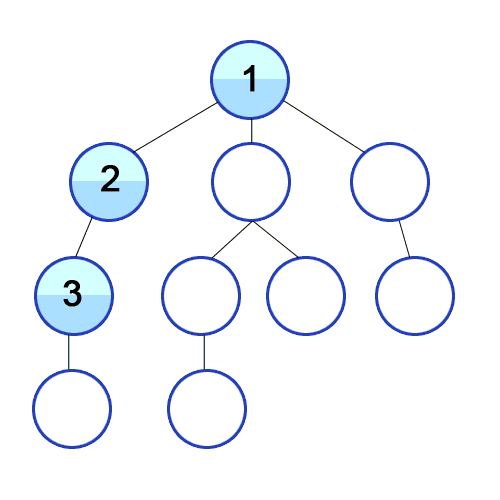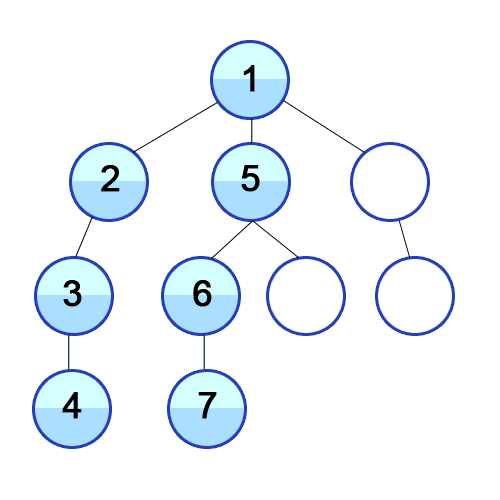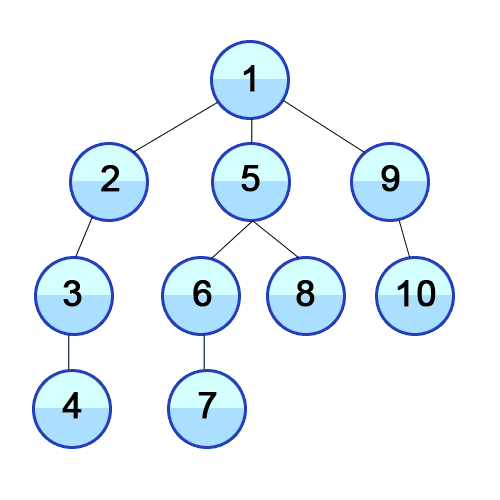
깊이 우선 탐색 (DFS) 는 너비 우선 탐색과 함께 코딩 테스트 출제 빈도가 높은 전략입니다. DFS 는 그래프에서 A 노드를 방문하고, 방문한 A 노드와 연결된 B 노드를 방문하고, 방문한 B 노드와 연결된 C 노드를 방문하는 과정을 반복해서 그래프의 모든 노드를 방문합니다. 너비 우선 탐색과 달리 굉장히 직관적인 탐색 방법입니다. DFS 을 사용하여 그래프를 탐색할 때 무한 반복을 조심해야 합니다. 만약 그래프에 사이클이 있다면 무한히 탐색을 반복하게 됩니다. 따라서 이미 방문한 노드를 기록하고 탐색할 때 방문했는지 안했는지를 확인해야 무한 반복을 피할 수 있습니다.
DFS 전략으로 푸는 대표적인 문제 유형
- 노드 사이 간 거리가 다른 최단 경로 탐색 문제 (다익스트라 알고리즘도 DFS 전략을 사용합니다.)
- 그래프 최소 신장 트리 문제
- 그래프 내 사이클 탐색 문제
- 미로 탈출 문제
전략 기본 순서
- '노드' 클래스를 만든다.
- 입력된 데이터를 정리해서 각 노드를 생성하고 연결하여 그래프를 만든다.
- 노드 방문 여부를 기록할 자료 구조를 준비한다.
- 그래프를 탐색할 회귀 함수를 작성한다.
- 그래프의 시작 노드를 큐에 추가하고 탐색을 시작한다.
- 각 탐색마다 탐색을 중지할지 평가한다.
- 데이터를 처리하고 방문으로 표시한다.
- 현재 방문 중인 노드의 이웃 노드를 회귀 함수로 탐색한다.
1 번부터 4 번까지는 탐색 전에 준비하는 과정이고 문제에 따라 간단하게 배열로만 처리할 때도 많습니다. 대부분 6 번부터 8 번까지가 문제를 풀기 위해 탐색을 반복하는 과정입니다.
DFS 전략으로 문제를 풀면 다음과 비슷한 코드를 구현하게 됩니다.
class Node:
def __init__(self, value):
self.value = value
self.adjacent = []
def visit(node):
print(node.value)
def dfs(visited, node):
visited.append(node)
visit(node)
for adj in node.adjacent:
if adj not in visited:
dfs(visited, adj)너비 우선 탐색 (Breadth first search, BFS) 과의 차이
너비 우선 탐색 (Breadth first search, BFS)도 그래프 형태의 자료구조를 탐색하는데 '깊이' 대신 '너비'를 우선하여 탐색한다는 점이 다릅니다. DFS 와 BFS 코드는 유사하지 않습니다. DFS 는 재귀 함수가 핵심인 반면, BFS 는 큐를 활용하여 탐색을 진행합니다.
인접 행렬로 표현된 그래프의 경우
그래프를 표현하는 방법은 크게 두 가지가 있습니다.
- 인접 리스트: 노드와 노드의 연결로 표현하는 방법
- 인접 행렬: 행렬의 행과 열로 연결을 표현하는 방법
인접 리스트로 표현한 그래프가 일반적으로 사용하기가 무난합니다. 왜냐하면 노드를 추가하고 삭제하기가 인접 행렬에 비해 편하기 때문입니다. 행렬의 경우 크기가 이미 정의되어 있는 구조라, 노드를 추가하게 되면 새로운 행렬을 추가해야만 합니다. 특히 중간에 노드를 추가하기 라도 하면 복잡해지기 시작합니다.
하지만 코딩 테스트 문제의 경우 시간 제약 때문에 그래프의 크기가 변하는 문제가 출제되는 경우도 적고, 행렬로 표현하면 디버깅할 때 보기 편하다는 장점이 있어서 무조건 인접 리스트로 그래프를 만들어 문제를 푸는 것보다는 문제가 제공하는 데이터의 형태에 따라 그래프를 만드는게 좋습니다.
예를 들어 다음과 같이 입력이 주어지는 경우는 인접 리스트가 더 적합할 수 있습니다.
1 2
4 2
2 3
4 5하지만 다음과 같이 입력이 주어지는 경우라면 인접 행렬이 더 적합할 수 있습니다.
4
0 0 1 1
0 0 0 0
1 0 0 1
1 0 1 0'Develop > 코딩인터뷰' 카테고리의 다른 글
| [코딩인터뷰] 백준 2468번 (0) | 2021.03.24 |
|---|---|
| [코딩인터뷰] 알고리즘 시간 복잡도 분석 방법 (0) | 2021.03.23 |
| [코딩인터뷰] 백준 2638번 (0) | 2021.03.22 |
| [코딩인터뷰] 백준 2146번 (0) | 2021.03.22 |
| [코딩인터뷰] 백준 16236번 (0) | 2021.03.21 |
꾸준히 노력하는 개발자 "김예건" 입니다.